关于音响有限障板的探讨，一些细思极恐的问题

关于音响有限障板尺寸，常听到的算法是波长的1/4，所以如果设计是给低音到100Hz用的障板，尺寸将是：

由C=L*f，343=L*100=L=3.43(m)

1/4L=0.8575(m)即85.75cm

然而这个1/4L的建议值是怎么来的？似乎找不太到，合不合理，也无法验证，只能耳听为凭。

下面我将先抛开一般建议值，从一些基本原理开始，重新检视这个问题。

所以必须要隔开振膜前后的声音。要隔开振膜前后声音的最简单方式有：(1)无限障板，(2)密闭式音箱。

但是：

(1)无限障板在一般聆听环境很难达成，除非嵌入墙面并且墙后是无限空旷的状况。

(2)密闭式音箱曾是最常见的作法，但是低频低落。在同样单体下，装在密闭式音箱的F0比装在障板上的F0要高。

无限障板与密闭式音箱这两者都单纯只是隔开振膜前后的声音，而无法利用振膜后面发出的声音。

为了利用振膜后发出的声音，于是又有所谓传输线式音箱等等的设计，利用声音传递距离的不同，将原本反相的声音作相位调整。有限障板的情况基本上也是如此，让声音必须绕过障板，进而改变其相位，与直接音造成干涉。

根据Huygens–Fresnelprinciple，喇叭振膜后面的声音的路径如下图，即AB+BC或AB'+B'C：

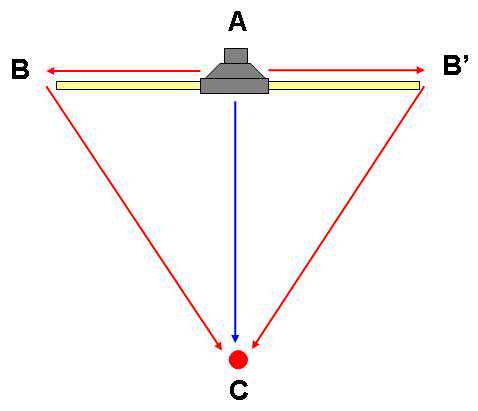
假设B跟B'与A跟C的相对距离是一样的，省略B'不看，那么听者听到的是由路径AC来的直接音加上由路径AB+BC而来的反相声音。

两者的传递距离分别为AC跟AB+BC

利用三角函数计算，AB+BC=AB+((AB^2+AC^2))^0.5

假设人耳与喇叭距离3m，即上图的AC=3；障板宽86cm，即上图AB=0.43，代入上面两式，可得：

AC=3(m)

AB+BC=3.46(m)

两者距离差为0.46m，对应到100Hz(L=3.43m)，约为0.134倍的波长，与原本预期的0.5倍波长有落差。

模拟100Hz的波形图(忽略距离的衰减量)为：

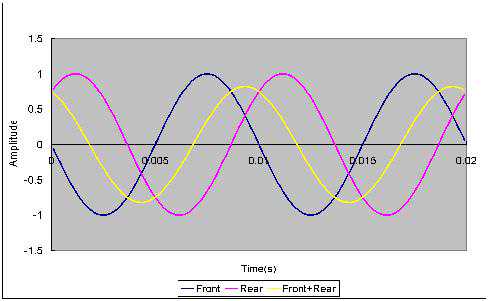
显示两者成破坏性干涉。

在同样聆听距离下，改变障板宽度，并以单频音仿真对频率响应图，可得：

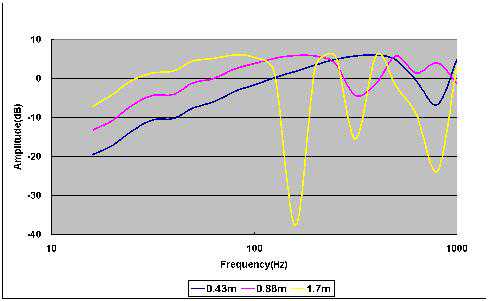
由此可知，原则上障板尺寸越大(显然要比1/4L大得多)，可将F0越往下拉，但是：

(1)障板尺寸越大，就越要考虑因距离造成的衰减(能量损耗加上空间散布)，来自振膜后的声音会比理想状态小

(2)可能会造成其他频率的不规则破坏性干涉，但必须配合这颗喇叭振膜后声音的高频方向性来看，如果方向性够强，或许没差